嵌套for循环中的迭代次数？

所以我一直在寻找从课本验证码：嵌套for循环中的迭代次数？

for (int i=0; i<N; i++) 
    for(int j=i+1; j<N; j++)

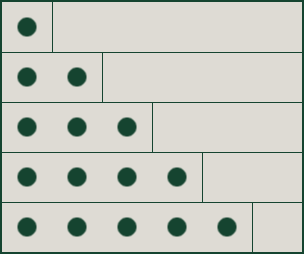
笔者表示，内部的for循环遍历了整整N *（N-1）/ 2次，但给出了他是如何到达没有依据到这样的等式。我明白N *（N-1），但为什么除以2？我自己运行代码，当N为10时，内部循环重复45次（10 * 9/2）。

我的代码混乱围绕我和尝试了以下（只分配我到j）：

for (int i=0; i<N; i++) 
    for(int j=i; j<N; j++)

随着N = 10，这导致55所以我无法理解基础数学这里。当然，我可以插入所有的价值观，并通过解决问题的方法来解决问题，但我觉得有一些必不可少的东西我很想念。你如何提出一个方程来描述我刚刚构建的for循环？有没有办法做到这一点，而不依赖于产出？非常感谢任何帮助，谢谢！

来源

2010-07-06 Sam

http://en.wikipedia.org/wiki/Arithmetic_series – 2010-07-06 19:38:10

请注意，外环中有'n'，内循环中有'N'。这是一个错字吗？因为如果这不是一个错字，答案是不同的。 – IVlad 2010-07-06 19:41:48

对不起，它应该是一个资本N – Sam 2010-07-06 19:46:04

想一想每次外层循环迭代时会发生什么。第一次，i == 0，所以内循环开始于1并运行到N-1，这总共是N-1迭代。下一次通过外循环，i已增加到1，所以内循环开始于2并运行到N-1，总共N-2迭代。并且该模式继续：第三次通过外部循环，您将获得N-3迭代，第四次通过，N-4等等。当您进入外部循环的最后一次迭代时，i == N-1，因此内部循环以j = N开始并停止立即。所以这是零迭代。

迭代的总数是所有这些数字的总和：

(N-1) + (N-2) + (N-3) + ... + 1 + 0

看它的另一种方式，这仅仅是一个正整数从1到N-1的总和。这个和的结果被称为（N-1）三角形数字和Wikipedia解释了如何找到第n个三角形数的公式为n（n + 1）/ 2。但在这里你有（N-1）个三角号，所以如果你设置n=N-1，你

(N-1)(N-1+1)/2 = N(N-1)/2

来源

2010-07-06 19:40:18

谢谢你，这正是我一直在寻找！ – Sam 2010-07-06 19:44:41

http://everything2.com/title/Gaussian+formula – Unreason 2010-07-07 08:54:03

看看内部（j）循环为i的每个值运行多少次。当N = 10时，外（i）循环运行10次，并且j循环应运行0,1,2,3,4,5,6,7,8和9次。现在您只需将这些数字加起来就可以看出内部循环运行的次数。您可以用公式N（N-1）/ 2将数字从0到N-1相加。这是对adding the numbers from 1 to N的着名公式的轻微修改。

对于视觉辅助，你可以看到为什么1 + 2 + 3 + ... + N = N *（N + 1）/ 2

Sum from 1 to N

来源

2010-07-06 19:35:25

这里有一个很好的视觉证明：http://www.9math.com/book/sum-first-n-natural-numbers – 2010-07-06 19:38:29

@Harold：你称之为*视觉*证明？请看我自己的[Six Visual Proofs]（http://www.billthelizard.com/2009/07/six-visual-proofs_25.html）＃4。 ;） – 2010-07-06 19:47:11

刚刚检出了您的六个视觉证明以及您网站上的其他几个网页...出色的工作。谢谢。 – NealB 2010-07-06 20:27:53

你在看嵌套循环，其中外部循环运行N次和内部循环(N-1)。你实际上将总和加起来为1 + 2 + 3 + ....

N * (N+1)/2是数学中的“经典”公式。年轻的卡尔高斯，后来成为着名的数学家，被授予了课堂上的繁忙工作：将数字从1增加到100.老师希望让孩子们忙一小时，但卡尔几乎立即提出了答案：5050.他解释说：1 + 100; 2 + 99; 3 + 98; 4 + 97;等等，最多50 + 51.这是50个和101个。你也可以看到（100/2）*（100 + 1）;那就是/2的来源。至于为什么它是（N-1）而不是我提到的（N + 1）......这可能与从1开始而不是从0开始有关，它会从内循环中删除一个迭代，I认为。

来源

2010-07-06 19:37:42

+1好的解释，你也是从1开始而不是从0开始。 – 2010-07-06 19:41:00

不应该是“高达50 + 51”吗？ – 2013-02-20 22:08:43

@Luca Molteni：绝对好，赶上！这被忽视超过2年;） – 2013-02-22 08:18:31

如果算上内部循环的迭代中，您可以：

为了得到总的迭代任意数量的，你可以“包装”的数字周围像这样：

0 1 2 3 4 
9 8 7 6 5

现在，如果我们增加这些列的每一个中，所有的一个dd到9（N-1），并且有5（N/2）列。很明显，对于任何偶数N，我们仍然会得到N/2列，每列加起来为（N-1）。因此，当迭代总数为偶数时，总迭代次数总是（N/2）（N-1），这（归功于交换属性）我们可以改写为N（N-1）/2。

如果我们对奇数次迭代做了同样的处理，我们会有一个“奇数”列无法配对。在这种情况下，我们可以忽略'0'，因为我们知道在任何情况下都不会影响整体总和。例如，让我们考虑N = 9而不是N = 10。为此，我们得到：

1 2 3 4 
8 7 6 5

这使我们（N-1）/ 2列（9-1 = 8,8/2 = 4），每个加起来N，所以总和将是N *（N-1）/ 2。尽管我们稍微有所不同，但当N为偶数时，这与上述公式完全匹配。同样，不管我们使用的列的数量是多少（即迭代的总次数），这似乎是非常明显的。

对于任何N（奇数或偶数），从0到N-1的数字总和为N *（N-1）/ 2。

来源

2010-07-06 19:56:41

嵌套for循环中的迭代次数？

回答

相关问题